はじめに
免震構造は免震層にエネルギー(変形)を集中させる明快な構造である。このため地震により建物に入力された全てのエネルギーを免震層で吸収することになる。入力エネルギーと吸収エネルギーのバランスを考慮することで免震層の応答変位や応答せん断力係数を予測する方法が確立されている。これを包絡解析法1 2と呼ぶ。
包絡解析法の導出と適用性について紹介するとともに、エネルギーの釣り合いからわかる免震構造の応答特性についても紹介する。
入力エネルギーの計算
建物下部にアイソレータとダンパーを配置した免震層を有する免震建物を対象とする。アイソレータとダンパーのみが地震エネルギーを吸収するものとし、上部構造は地震エネルギーの吸収を行わないものとする。この時、エネルギーの釣り合い式は次式で表される。
$$ W_e (t)+W_p (t)=E(t) \tag{1} $$
ここで、\( W_e (t) \)は時刻\( t \)までのアイソレータの弾性歪みエネルギー、\( W_p (t) \)はダンパーの消費エネルギー、\( E(t) \)は地震による入力エネルギーである。図1に示すような1自由度系モデルへ地動加速度\( \ddot{z} \)が作用する場合の地震入力エネルギーは、次式に示すように時々刻々の慣性力(\( M\ddot{z} \))に応答の変位増分(\( dx \))を乗じて積分することで計算できる。
$$ E=-\int M\ddot{z}\cdot dx $$
地震入力エネルギー\( E \)は建物質量\( M \)で規準化されエネルギーの等価速度\( V_E \)に変換して用いられることが多い。
$$ V_E = \sqrt{\frac{2E}{M}} $$
地震入力エネルギーの等価速度\( V_E \)と周期の関係を示したものがエネルギースペクトルである。図2には粘性系や履歴系に対して求められたエネルギースペクトルの例を示す。エネルギースペクトルは一種の応答スペクトルであるが、通常の応答スペクトルでは減衰が大きくなるに従い応答値は減少するのに対し、エネルギースペクトルではある一定値に収束する。すなわち、減衰が0の振動系への入力エネルギーは非常に変動が大きいものの、粘性減衰が増える、あるいは塑性化が大きな系になれば入力エネルギーが平滑化されることがわかっている。
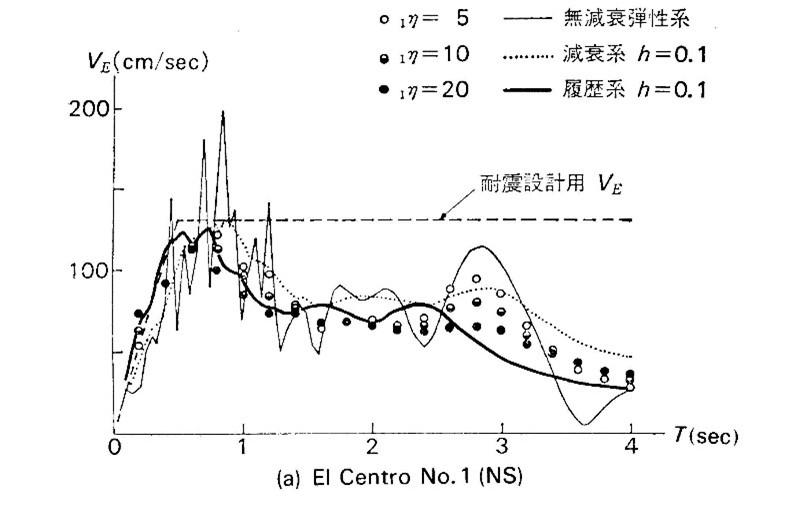
文献1 2ではこの様なエネルギースペクトルに基づいて設定された設計用エネルギースペクトルも提案されている。設計用エネルギースペクトルは粘性減衰10%の弾性振動系の入力エネルギーとして求めるこができる。ほとんどの観測地震波のエネルギースペクトルは振動系の周期が長くなれば低下する傾向にある。しかし、地盤の種別や地震波の特性によっては、長周期領域での入力エネルギーがどのようになるかは予測できないため、設計用スペクトルとしては長周期領域で一定値、短周期領域で一定の勾配をもつバイリニアタイプのスペクトルが提案されている。このため免震構造の周期領域では\( V_E \)は一定値となり、地盤種別ごとに\( V_E \)=120, 150, 200, 300cm/sが提案されている。免震構造設計指針には様々な観測地震波に対するエネルギースペクトルが示されているので参照されたい。これまでの時刻歴応答解析でよく利用されてきたEL CENTRO波、八戸波を50cm/sに規準化した入力波の入力エネルギーの速度換算値は150cm/s程度、兵庫県南部地震の際の震源地近傍での観測波では、300cm/s程度であったとの報告もある。
入力エネルギー量を時刻歴応答解析により求め、入力エネルギーと時間との関係を描くことができる。弾性振動系への入力エネルギーは最大の変位応答が発生する時刻で最大の入力エネルギーを示す。一方、減衰の大きな系や塑性化が進行する系では入力エネルギーは単調増加となり、入力エネルギーの大部分が減衰あるいは塑性ひずみによる吸収エネルギーとなる。
(1)式は免震層が最大変形を示す時刻\( t=t_m \)においても当然成立する。一般に塑性化の程度が大きな系では最大変形を示す時刻での入力エネルギー量\( E(t_m) \)は最大値をとらないため、地震終了時\( (t=t_0) \)の入力エネルギー総量\( E( t_0 ) \)は\( E( t_m ) \leq E( t_0 ) \)となる。従って、(1)式において\( t=t_m \)として免震層の最大変位を予測する時、右辺を\( E( t_0 ) \)で置き換えることは安全側の予測を行うことにつながる。しかし、地震波の特性によっては\( V_E ( t_0) \)と\( V_E ( t_m) \)の差が大きくなる場合があり、応答予測の精度を低下させる原因となる。
免震層の応答予測式
ここでは、図3に示すようにアイソレータが弾性、ダンパーが完全弾塑性型の復元力特性を有する場合を対象とする。免震部材には高減衰ゴム系積層ゴムや鉛プラグ型積層ゴムなどのようにダンパーを一体としたデバイスも用いられるが、これらの復元力特性は基本的にバイリニア型でモデル化されており、ここで紹介する方法に適用可能である。また様々な特性を有するデバイスが実用化されているものの、最も単純な復元力モデルを用いて検討しておくことは有効であり適用性も高い。
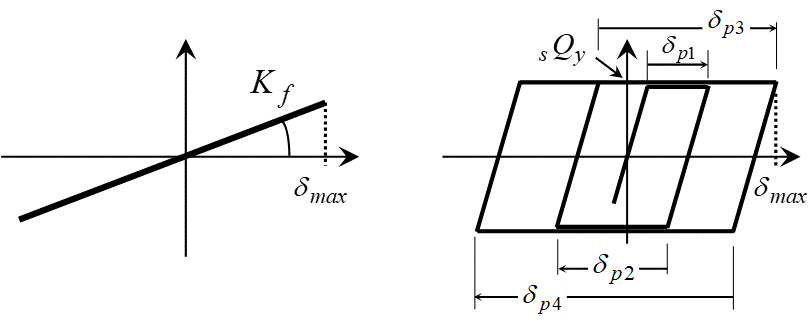
最大変形を生じるときのアイソレータとダンパーの吸収エネルギー量はそれぞれ次式で表せる。
\begin{align}
W_e ( t_m ) & = \frac{1}{2} K_f \delta^2_{max} \tag{2a} \\
W_p ( t_m ) & = {}_s Q_y \cdot {}_s \delta _p \tag{2b}
\end{align}
ここで、\( K_f \)はアイソレータの水平剛性、\( \delta_{max} \)は免震層の最大変形であり、\( W_e \)はアイソレータの弾性部分の履歴面積を算出している。また、\( {}_s Q_y \)はダンパーの降伏耐力、\( {}_s \delta _p \)はダンパーの累積塑性変形量である。累積塑性変形量は塑性化領域の変形量(絶対量)を加算することで求められる。
$$ {}_s \delta _p = \sum \delta_{pi} $$
\( W_p \)は、降伏体力と累積塑性変形量を乗じることで長方形の履歴面積を求めている。
累積塑性変形量と最大変形量の関係は、変数\( \kappa \)を導入することで次式のように表せる3。
$$ {}_s \delta _p = \kappa ( \delta _{ave} – {}_s \delta _y ) \tag{3} $$
ここで、\( \delta _{ave} \)は正側と負側の最大変形の平均値、\( {}_s \delta _y \)はダンパーの降伏変位、\( \kappa \)は累積塑性変形量と最大変形量の比率である。\( \delta _{ave} \)に比べ\( {}_s \delta _y \)が十分に小さく、\( \delta _{ave} \)と\( \delta _{max} \)に大きな差が無ければ(正側と負側に同じ程度の最大変形が発生していれば)、(3)式は\( {}_s \delta _p = \kappa \delta _{max} \)と近似できる。
この近似式と(2)式を(1)式に代入すれば、次式が得られる。
$$ 4 \pi ^2 \left( \frac{ \delta _{max} }{ T _f } \right) ^2 + 2 \kappa g \alpha _s \cdot \delta _{max} = V ^2 _E $$
ここで、\( V_E \)は地震入力エネルギーの等価速度、\( M \)は建物総質量、\( g \)は重力加速度、\( T_f \)はアイソレータのみの水平剛性に基づいた周期で次式となる。
$$ T_f = 2 \pi \sqrt{ \frac{M}{K_f} } $$
これを\( \alpha _s \)について解けば、$$ \alpha _s = \frac{ {}_s Q _y}{Mg} = \frac{1}{2 \kappa g} \left( \frac{V ^2 _E}{\delta _{max} } – \frac{4 \pi ^2 \delta _{max} }{T ^2 _f} \right) $$が得られ、これにアイソレータのせん断力係数\( \alpha _f \)を加えることで、免震層の最大せん断力係数(以下、ベースシア係数)\( \alpha _1 \)が次式のように求められる。
$$ \alpha _1 = \alpha _f + \alpha _s = \frac{ 4 \pi ^2 \delta _{max} }{gT ^2 _f} \left( 1 – \frac{ 1 }{ 2 \kappa } \right) + \frac{ V ^2 _E }{ 2 \kappa g \delta _{max} } \tag{4} $$
なお、アイソレータの最大せん断力係数\( \alpha _f \)は、次式で表せる。
$$ \alpha _f = \frac{ K _f \delta _{max} }{Mg} = \frac{4 \pi ^2 \delta _{max} }{gT ^2 _f} $$
同様に、免震層の最大変形量\( \delta _{max} \)は次式で求められる。
$$ \delta _{max} = \frac{ \kappa g \alpha _s T ^2 _f}{ 4 \pi ^2 } \left\{ -1 + \sqrt{ \left( \frac{ 2 \pi V _E }{ \kappa g \alpha _s T _f } \right) ^2 + 1 } \right\} \tag{5} $$
応答予測図
図4に\( T_f \)を4秒とした時の\( \alpha _1 \)と\( \delta _{max} \)の関係を(4)式に基づいて示す。なお、\( \kappa \)については平均的に8を使うことができると言われており3、図4でも\( \kappa \)=8を用いている。\( \kappa \)=8は、最大変形が起こるまでにダンパーが最大変形下での履歴ループに換算して2サイクル分のエネルギーを吸収したことに対応している。同図(a)は、\( T_f \)=4秒に固定した時のベースシア係数と免震層の変形の関係を描いている。下に凸の曲線は入力エネルギー量\( V_E \)が一定の時の関係であり、右上がりの直線はダンパーの降伏せん断力係数が一定の時の関係である。\( V_E \)の大きさによりベースシア係数が極小となる変形量は変化するものの、\( V_E \)=150cm/sでは20~30cm程度、\( V_E \)=300cm/sでは40cm程度の変形となる。なお、免震周期が短くなれば、免震層の変形は小さくなるものの、ベースシア係数が上昇することになる。様々な\( T_f \)に関して同様の図を描いてみると免震構造の特性をより良く理解できると考える。同図(b)(c)では\( V_E \)=150cm/sおよび200cm/sと一定にした時の関係図である。免震周期が長くなるに従って、ベースシア係数が小さくなることがわかる。また、ダンパーの降伏せん断力係数、すなわち減衰が小さいと免震層の変形は大きくなり、減衰が大きすぎると変形は小さくなるもののベースシア係数が急激に大きくなる。このように想定される入力地震動の大きさに対して免震構造の応答を最小にするアイソレータの周期とダンパーの減衰量が存在することになる。
図4 免震層のベースシア係数と最大変位の関係
ベースシア係数の最小値\( \alpha _{1min} \)は、
$$ \alpha _{1min} = \frac{ \sqrt{15} \pi }{4g} \frac{V _E}{T _f} \tag{6} $$
となり、免震周期\( T_f \)と入力エネルギーの速度換算値\( V_E \)にしか影響されないことがわかる。この時のアイソレータとダンパーのせん断力係数\( \alpha ^{opt} _s \)と\( \alpha ^{opt} _f \)、及び変形量\( \delta ^{opt} _{max} \)は
\begin{align}
\alpha ^{opt} _s & = \frac{ 7 \pi }{ 4 \sqrt{15} g } \frac{V _E }{ T _f } \\
\alpha ^{opt} _f & = \frac{ 8 \pi }{ 4 \sqrt{15} g } \frac{V _E }{ T _f } \tag{7} \\
\delta ^{opt} _{max} & = \frac{ 1 }{ 2 \sqrt{15} \pi } T _f V _E
\end{align}
となる。上式よりアイソレータとダンパーのせん断力の比率\( \alpha _f \) / \( \alpha _s \)が8 / 7とほぼ同じせん断力を負担している時が最適な状態であることが判る。図5には(6)式と(7)式から得られる免震層のベースシア係数と水平変形を示す。免震周期がのびるほど、応答変形は大きくなるものの、ベースシア係数は小さくなり、入力エネルギーの大きさによる変化も小さくなる。
ベースシア係数の極小値をとる変位は周期が伸びる程、\( V_E \)が大きくなる程増加するが、\( V_E \)=300cm/sにおいても40cm程度の変形を見込んでおけば良いことがわかる。また免震建物をどの程度の地震入力エネルギー量に対して設計しているのか、又設計されているのかを次式により逆算することも性能を表す1つの指標になると思われる。
$$ V _E = \sqrt{g (2 \kappa \alpha _s + \alpha _f ) \delta _{max} } \tag {8} $$
この様に包絡解析法は免震建物の入力と応答の関係を容易に把握することを可能にする。
予測式の検証
エネルギーの釣り合いによる応答予測の精度を確認するために1質点系モデルによる応答解析を実施した。解析モデルの周期\( T_f \)は1~6sec、降伏変位\( _s \delta _y \)は1cmとした。入力地震波は9種類で、El Centro(NS), Taft(EW), 八戸(NS)は最大速度を50cm/sに規準化している。その他のMexico地震やNorthridge地震などの観測波は原波形を用いた。
解析結果より、(3)式で定義される\( \kappa \)は周期の影響をあまり受けていないが、入力波の特性の影響を受け2~15程度まで変動する。大部分の場合\( \kappa \)は8以下となっている。一方、\( V_E(t_m )/V_E(t_0) \)は周期3sec以上では0.5~0.8程度であり、\( \kappa \)が小さな値をとる場合ほど低い値を示している。なお、入力エネルギーの等価速度\( V_E(t_0) \)は周期3sec以上ではほぼ一定値を示し、100~300cm/sの範囲にあった。
図6には免震層最大変位と(5)式による予測値の関係を示す。(5)式の適用では\( \kappa \)=8、\( V _E \)=\( V _E ( t _0 ) \)とした。なお、ここでの\( t_0 \)は応答解析終了時としている。同図より、特にSylmar波(Northridge地震)の場合に予測値が小さくなっている以外は、予測値はほぼ安全側の予測になっていることが判る。
エネルギーの釣り合いに基づいた応答予測では、実際の応答が\( \kappa \)=8である場合でも\( V_E(t_m )/V_E(t_0) \)の値によっては予測値の精度は変化する。Northridge地震のような地震波の場合、\( \kappa \)は4程度で\( V_E(t_m )/V_E(t_0) \)も0.8~1.2と大きかったために、予測値の精度が低下したと考えられる4。\( \kappa \)を4, 8, 16と変化させた場合の応答値の変動を図7に示す。同図より、\( \kappa \)が8よりも大きければ応答値は小さくなり、\( \kappa \)が小さければ応答値は大きくなることが分かる。想定する地震動の特性によっては応答の予測値が変動することを考慮しておく必要がある。
図7 \( \kappa \)による応答予測の変動
時刻歴応答解析では個々の地震波の特性に応じて応答結果が変化するが、エネルギーの釣り合いによる応答予測では幾つかの仮定に基づく多少の変動はあるものの、包括的に応答を評価することが可能であり、免震建物(通常の建物も含め)の応答特性を誤ることなく評価できる手法であると言える。
ここで紹介したエネルギーの釣り合いに基づいた地震時応答予測手法は、免震建物の最大応答を簡単に求めることができ、さらに免震周期やダンパーの量に応じて応答値がどのように変動するかを把握することを可能とする。こういった手法で時刻歴応答解析結果を検証したり、設計した建物がどの程度までの地震エネルギーを吸収できるのかをチェックすることに活用されることを期待したい。なお、免震構造設計指針(日本建築学会編、2013年)では、ここで紹介した手法を拡張して、オイルダンパーを使うような場合の応答予測についても示されているので参考にしてほしい。
